CitruXonve's another far end

#Grids

Time Limit: 10000/5000 MS (Java/Others)
Memory Limit: 65535/65535 K (Java/Others)

##Problem Description

　　度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

##Input

　　第一行为数据组数T(1< =T<=100000)。
　　然后T行，每行为一个数N(1< =N<=1000000)表示长方形的大小。

##Output

　　对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

##Sample Input

2
1
3

##Sample Output

Case #1:
1
Case #2:
5

##Hint

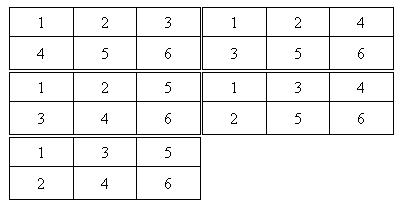
对于第二组样例，共5种方案，具体方案为：

##Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

---

引用维基百科的解释：

Cn is the number of standard Young tableaux whose diagram is a 2-by-n rectangle. In other words, it is the number of ways the numbers 1, 2, …, 2n can be arranged in a 2-by-n rectangle so that each row and each column is increasing. As such, the formula can be derived as a special case of the hook-length formula.

• 除法取模运算、Catalan数计算依赖于不同的推导，分别有多种不同写法，分别有不同的时间复杂度表现。

/**
 * Apr 3, 2016 9:54:01 PM
 * PrjName: hdu4828
 * @semprathlon
 */

import java.io.*;
import java.util.*;

public class Main {
    final static int maxn = 1000010, mod = 1000000007;
    static long inv[] = new long[maxn];
    static long a[] = new long[maxn];
    static long b[] = new long[maxn];
    static long C[] = new long[maxn];
    static long x, y;

    static void extgcd(long a, long b) {
        if (b == 0L) {
            x = 1L;
            y = 0L;
            return;
        }
        extgcd(b, a % b);
        long t = x;
        x = y;
        y = t - a / b * y;
    }

    static void get_inv(int maxn, long mod) {
        inv[1] = 1;
        for (int i = 2; i < maxn; i++) {
            // inv[i] = (mod - mod / i) * inv[(int) (mod % i)] % mod;

            inv[i] = (int) cal_inv(i, mod);
        }
    }

    static long cal_inv(long n, long mod) {
        extgcd(n, mod);
        return x < 0L ? (x + mod) % mod : x % mod;
    }

    static long pow_mod(long n, long m, long mod) {
        long res = 1L;
        n %= mod;
        while (m > 0L) {
            if ((m & 1L) > 0L)
                res = res * n % mod;
            n = n * n % mod;
            m >>= 1;
        }
        return res;
    }

    static long div_mod(long n, long m, long mod) {
        // return n * pow_mod(m, mod - 2, mod) % mod;
        // return n * pow_mod(m, phi(mod) - 1, mod) % mod;
        return n * inv[(int) m] % mod;
    }

    static void get_Catalan(int maxn) {
        a[1] = 2;
        b[1] = 1;
        C[1] = 1;
        for (int i = 2; i < maxn - 1; i++) {
            /*
             * a[i] = a[i - 1] * ((i << 1) - 1) % mod * (i << 1) % mod; a[i] =
             * div_mod(a[i], i, mod); a[i] = div_mod(a[i], i, mod); b[i] = b[i -
             * 1] * ((i << 1) - 1) % mod * (i << 1) % mod; b[i] = div_mod(b[i],
             * i + 1, mod); b[i] = div_mod(b[i], i - 1, mod); C[i] = a[i] -
             * b[i]; if (C[i] < 0) C[i] += mod;
             */
            C[i] = C[i - 1] * ((i << 2) - 2) % mod;
            C[i] = div_mod(C[i], i + 1, mod);
        }
    }

    public static void main(String[] args) throws IOException {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        get_inv(maxn, mod);
        get_Catalan(maxn);
        int T = in.nextInt(), cas = 0;
        while (T-- > 0) {
            int n = in.nextInt();
            out.println("Case #" + (++cas) + ":");
            out.println(C[n]);
        }
        out.flush();
        out.close();
    }

}